颜色映射归一化

默认情况下,使用颜色映射的对象会将颜色映射中的颜色从数据值 vmin 到 vmax 线性映射.例如:

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

会将 Z 中的数据从 -1 到 +1 线性映射,因此 Z=0 将在颜色映射 RdBu_r 的中心(在本例中为白色)给出一种颜色.

Matplotlib 分两步完成此映射,首先进行从输入数据到 [0, 1] 的归一化,然后映射到颜色映射中的索引.归一化是在 matplotlib.colors() 模块中定义的类.默认的线性归一化是 matplotlib.colors.Normalize() .

将数据映射到颜色的 Artist 传递参数 vmin 和 vmax 以构造 matplotlib.colors.Normalize() 实例,然后调用它:

>>> import matplotlib as mpl
>>> norm = mpl.colors.Normalize(vmin=-1, vmax=1)
>>> norm(0)
0.5

但是,在某些情况下,以非线性的方式将数据映射到颜色映射是有用的.

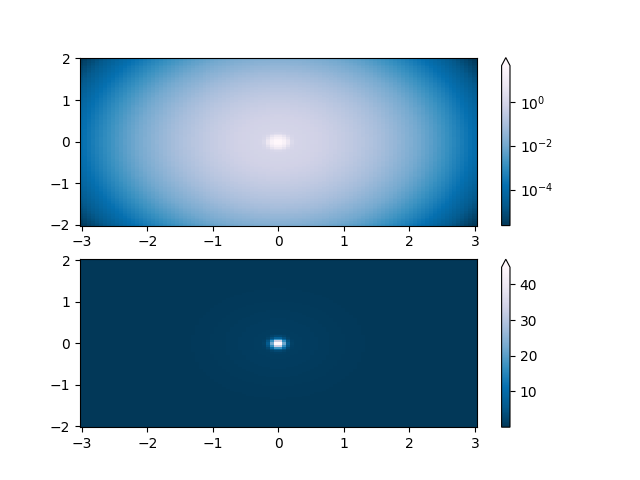
对数

最常见的转换之一是取其对数(以 10 为底)来绘制数据.此转换对于显示不同尺度上的变化很有用.使用 colors.LogNorm 通过 \(log_{10}\) 归一化数据.在下面的示例中,有两个峰,一个比另一个小得多.使用 colors.LogNorm ,可以清楚地看到每个峰的形状和位置:

import matplotlib.pyplot as plt
import numpy as np

from matplotlib import cm
import matplotlib.cbook as cbook
import matplotlib.colors as colors

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale, so we see both hump and spike. A linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

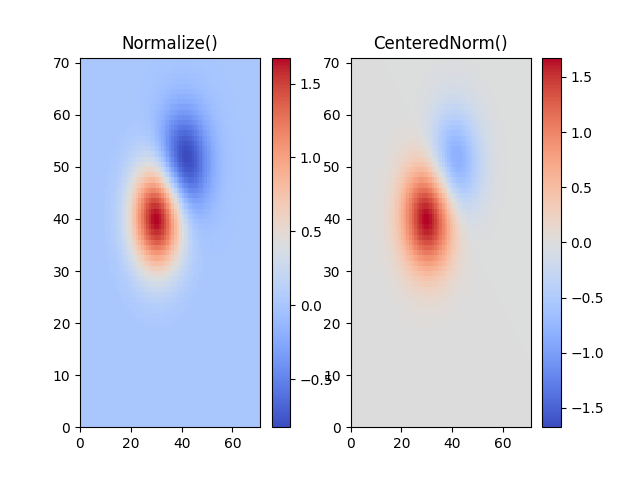
居中

在许多情况下,数据围绕中心对称,例如,围绕中心 0 的正负异常.在这种情况下,我们希望中心映射到 0.5,并且与中心偏差最大的数据点映射到 1.0(如果其值大于中心),否则映射到 0.0.范数 colors.CenteredNorm 自动创建这样的映射.它非常适合与发散颜色映射结合使用,该颜色映射使用在中心以不饱和颜色相遇的不同颜色边缘.

如果对称中心与 0 不同,则可以使用 vcenter 参数设置它.对于中心两侧的对数缩放,请参见下面的 colors.SymLogNorm ;要对中心上方和下方应用不同的映射,请使用下面的 colors.TwoSlopeNorm .

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

对称对数

类似地,有时会发生这样的情况:存在正数和负数的数据,但我们仍然希望对两者应用对数缩放.在这种情况下,负数也以对数方式缩放,并映射到较小的数字;例如,如果 vmin=-vmax ,则负数从 0 映射到 0.5,正数从 0.5 映射到 1.

由于接近零的值的对数趋于无穷大,因此需要在零附近线性映射一个小范围.参数 linthresh 允许用户指定此范围 (-linthresh, linthresh) 的大小.颜色映射中此范围的大小由 linscale 设置.当 linscale == 1.0(默认值)时,用于线性范围的正半部分和负半部分的空间将等于对数范围中的一个数量级.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

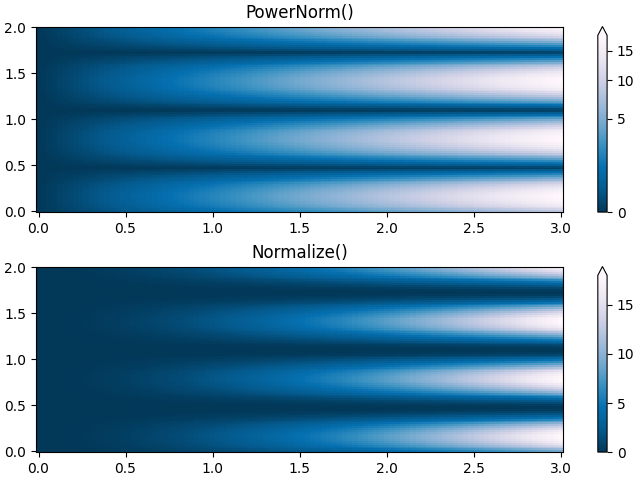
幂律

有时将颜色重新映射到幂律关系上很有用(即 \(y=x^{\gamma}\) ,其中 \(\gamma\) 是幂).为此,我们使用 colors.PowerNorm .它接受 gamma 作为参数(gamma == 1.0 将产生默认的线性归一化):

备注

对于使用这种类型的转换绘制数据,应该有一个很好的理由.技术观众习惯于线性和对数坐标轴以及数据转换.幂律不太常见,应该明确地告知观众已经使用了它们.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, layout='constrained')

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

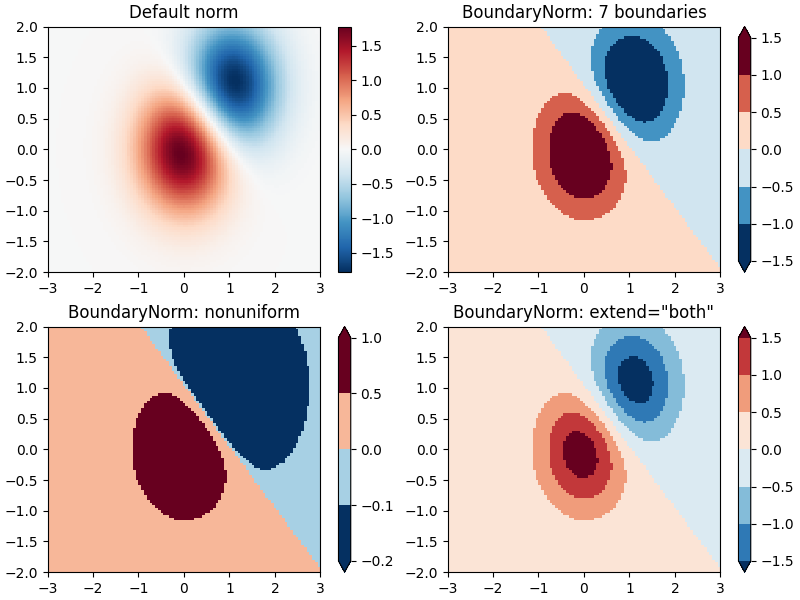
离散边界

Matplotlib 附带的另一个归一化是 colors.BoundaryNorm .除了 vmin 和 vmax 之外,它还接受数据要在其间映射的边界作为参数.然后,颜色在线性分布在这些"边界"之间.它还可以使用 extend 参数来添加上限和/或下限超出范围的值,以扩展颜色分布的范围.例如:

>>> import matplotlib.colors as colors
>>> bounds = np.array([-0.25, -0.125, 0, 0.5, 1])
>>> norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)
>>> print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

注意:与其他范数不同,此范数返回的值介于 0 到 ncolors-1 之间.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), layout='constrained')
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

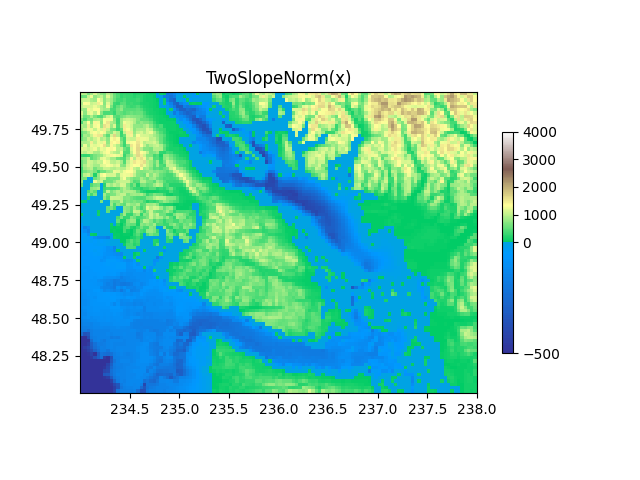
TwoSlopeNorm:中心两侧的不同映射

有时我们希望在概念中心点的两侧使用不同的颜色映射,并且我们希望这两个颜色映射具有不同的线性比例.一个例子是地形图,其中陆地和海洋的中心位于零,但陆地通常具有比水深度范围更大的海拔范围,并且它们通常由不同的颜色映射表示.

dem = cbook.get_sample_data('topobathy.npz')
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

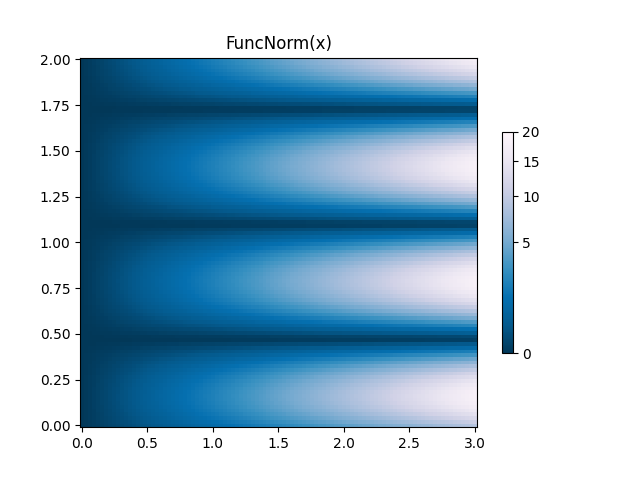
FuncNorm:任意函数归一化

如果上述范数没有提供您想要的归一化,您可以使用 FuncNorm 来定义您自己的归一化.请注意,此示例与幂为 0.5 的 PowerNorm 相同:

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

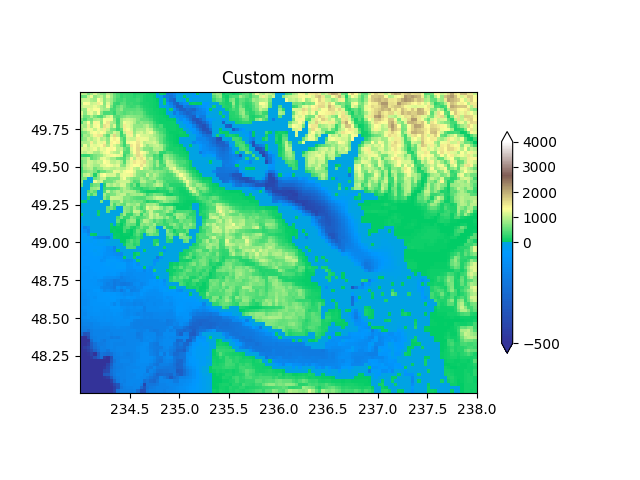
自定义归一化:手动实现两个线性范围

上面描述的 TwoSlopeNorm 是定义您自己的范数的一个有用的例子.请注意,为了使颜色条工作,您必须为您定义的范数定义一个逆:

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()